RESEARCH
頑健さを支えるしなやかさを計測する
現存の生物には38億年間続いてきた実績があります。その基本単位である細胞には継続を支える「頑健さ」があるはずと考え、調べる過程で浮かび上がったのは、意外にも「脆弱さ」の必要性でした。
1.生命システムが持つ2つの性質
20世紀中頃に生命現象をDNAから探る分子生物学が始まり、その後半には、生物の持つ全DNAを対象としたゲノム科学が大きく展開して、生命現象をつかさどる分子と各々の機能、それらの相互作用について非常に多くの知識が蓄積してきた。現在これらの知識を統合して、生命を分子レベルから一貫したシステムとして理解する努力がすすんでおり、システムバイオロジーと呼ばれている。それでは、システムとして生命を捉えることによって、初めて見えてくる生命の特性、いうなれば生命システムが持つ「生命らしさ」とは何だろう。
私は、その1つはダイナミクス(動態)がある事で、もう1つはロバストネス(頑健性)が高い事であると考えている。ダイナミクスは、生命の多種多様な動きや形を生み出すものであり、時間・空間的な機能を発揮する性質と言える。一方、ロバストネスは、様々な環境のもとで生きる生命のしなやかさと、したたかさを生み出すもので、擾乱にあらがって機能を維持する性質と言える。
現生するすべての生物は、自然界の淘汰圧のもとで適応・進化してきたのであるから、どれも高いロバストネスを持っているはずである。しかし、時々刻々変化するダイナミクスに対して、ロバストネスは、まさに擾乱に対して安定であるがゆえに表には見えてこない。ロバストネスは、ダイナミクスには必須でない要素も含めてシステム全体を見る事で初めて見えてくる性質なのだ。私は、生命の複雑さの中に潜み、ダイナミクスの陰に隠れて気づかれないロバストネスを研究する事で、これまで見えてこなかった生命の一面を浮き彫りにできると考えている。では、このつかみどころのなさそうなロバストネスは、どうすれば調べることができるのだろう。
2.“続く”を支える細胞周期システム
太古に細胞が生じてから、現在まで脈々と続く生命のふるまいの一つに細胞周期(図1)がある。私は、これが、生命のロバストネスを調べる恰好の対象になると考えている。細胞周期とは、細胞が成長し、その染色体DNAをコピーし、2つの娘細胞に均等に分配する一連の過程であり、そのダイナミックな細胞の変化は研究者を惹きつけてきた。そして、このシステムは生命38億年の歴史の中で高度に洗練され、十分に高いロバストネスを獲得しているはずだ。
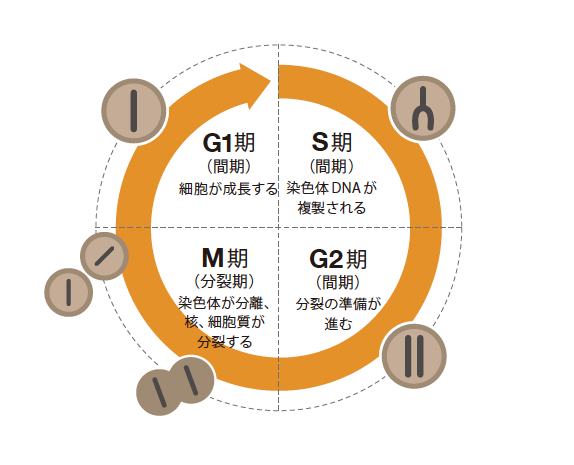
(図1) 細胞周期
細胞が増殖に際してくり返す周期で、4つの不可逆的な過程からなる。DNAを複製するS期、複製した染色体DNAが有糸分裂によって分離したのち細胞質が分裂するM期、そしてM期が終わりS期が始まるまでの間をG1期、S期が完了してからM期までの間をG2期と呼ぶ。
細胞周期のシステムを構成する制御因子については、真核単細胞生物である酵母を用いた解析がもっともすすんでおり、知識が蓄積している。それらを統合してシミュレーション解析を試みた「コンピュータ酵母」とも呼べる数理モデルも作られており、酵母の細胞周期研究には、複雑さの中から生まれるロバストネスを調べるのに十分な土壌がある。
真核生物の細胞周期に見られるダイナミクスは、サイクリン依存性キナーゼ(CDK)(註1)と呼ばれるタンパク質リン酸化酵素の活性が周期的に変動することで生じる。この基本のしくみにロバストネスがはたらいているかどうかを調べる前に、まずCDKのダイナミクスをシミュレーションした数理モデル*1を見てみよう(図2)。
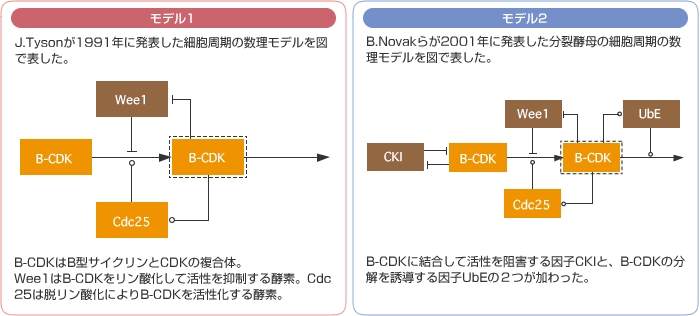
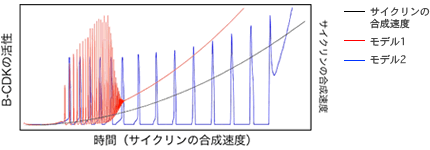
(図2) 細胞周期を再現する2つの数理モデルのシミュレーションによる比較
シミュレーションにより、サイクリンの発現量を徐々にふやした時に、B-CDKの活性の周期変動が維持される範囲を2つのモデルで比較した。
J Theor Biol. 2002 May 7;216(1):19-30.
Robustness as a measure of plausibility in models of biochemical networks. Morohashi M, Winn AE, Borisuk MT, Bolouri H, Doyle J, Kitano H.
モデル1(図2左上)はCDKのダイナミクスをシンプルに再現した数理モデルであり、CDK自身とその活性を直接制御する必要最小限の分子からなる。モデル2(図2右上)はこれに2つの分子が加わり、より実際の細胞システムに近い。この2つのモデルで、分子の一つサイクリンの発現量を徐々に上げていくと、モデル2は、モデル1よりも広い範囲で周期変動を維持できる(図2下)。つまり、2つの分子を加えることでロバストネスが高くなったのだ。同じダイナミクスを再現した2つの系だが、細胞内でおこる遺伝子発現量の変動という擾乱の操作により、システムの頑健さの違いを浮かび上がらせることができたと言える。ここから私は一歩進めて、シミュレーションでなく、実際に、細胞の中ではたらく遺伝子各々の発現量の変動の許容範囲を測ることができれば、生きた細胞システムが持つロバストネスの一端を知ることができるのではないかと考えた。
(註1) サイクリン依存性キナーゼ(Cyclin-Dependent Kinase, CDK)
タンパク質リン酸化酵素の一種。細胞周期ごとに合成と分解をくり返すタンパク質サイクリンと結合し、サイクリン-CDK複合体となって初めて活性をもつ。
3.生きた細胞のロバストネスを測る
実際の細胞で、発現する遺伝子の許容範囲を定量的に測ることは可能だろうか。これはそう簡単ではない。あれこれ考えた結果、「遺伝子発現をどこまで上げたら細胞は死ぬのか」という限界値を測定することにした。用いたのは出芽酵母(Saccharomyces cerevisiae)。この細胞では、多くの洗練された分子遺伝学の実験系ができている。それらを活用し、「遺伝子綱引き(genetic Tug Of War:gTOW)法」という実験手法を考えた。
ある遺伝子の発現量を上げる最も簡単な手段は、その遺伝子の細胞内あたりのコピー数をふやすことだ。これは、出芽酵母で一般的に用いられる多コピー型プラスミド(註2)に目的の遺伝子を組み込むことで実現できる。ただし通常この方法では、酵母が持つプラスミドのコピー数は偶然に左右され、定量には向かない。ここであるトリックを考えた。酵母ゲノムからロイシン合成酵素(LEU2 )を完全に欠失させておき、かわりにプラスミドに非常に活性の低いロイシン合成酵素(leu2d )を組み込んでおくのである(図3a)。この酵母をロイシンのない培地で培養すると、leu2d の数が多ければ多いほど生育にとってプラスとなるため、プラスミドのコピー数を引き上げる方向に選択がかかる。このプラスミドに、目的の遺伝子を同時に組み込んでおくのだ(図3b)。細胞が持つこの遺伝子の数は、細胞の死を招く限界値よりも低くならなければならない。つまり、ここで調べたい目的の遺伝子はプラスミドのコピー数を引き下げる選択圧となる。
最終的には両者の綱引きが釣り合ったところにプラスミドのコピー数が落ち着く。leu2d の力は一定なので、綱引きで決まる細胞内のプラスミドのコピー数は、目的の遺伝子の上限によって決まる(写真)。
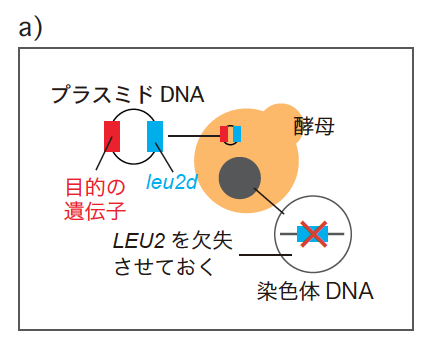
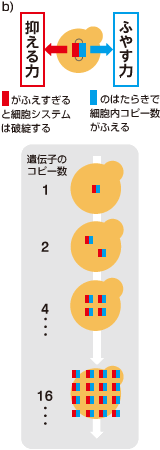
(図3) 遺伝子綱引き(genetic Tug Of War:gTOW)法
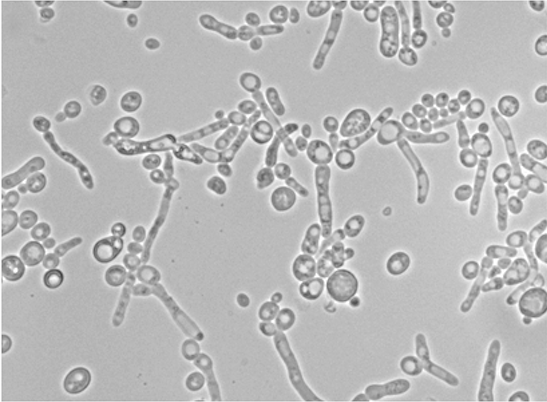
(写真) 出芽酵母による実験例
遺伝子SIC1 の場合は、コピー数32以上で分裂できず致死となった。
(註2) 多コピー型プラスミド
出芽酵母は核内の染色体DNAとは別に、小さな環状DNAのプラスミドをもつ。ここで遺伝子を導入するベクターとして用いる2μDNAプラスミドは、増殖と維持に必要な遺伝子を自前でもち、細胞内でコピー数をふやす。
4.細胞のロバストネス研究がもたらす2つの「問い」
gTOW法を用いて、出芽酵母の細胞周期にかかわる30個の遺伝子のコピー数の上限を測定した結果、2コピー以下から100コピー以上までバラバラだった(図4上)。つまり細胞周期には、少しの遺伝子発現の変化が致命的となるところもあれば、ちょっとやそっとの擾乱には、びくともしないところもあるのだ。この結果が実際の生物の持つロバストネスの特徴を反映したものだとすると、2つの「問い」が浮かび上がる。1つめの疑問は、コピー数の上限が低い遺伝子の存在である。先に述べたように、細胞周期などの生命システムは、ある程度高いロバストネスを持っているはずである。その中で、なぜ遺伝子発現の上昇を許さない脆弱な部分が残されているのだろうか。
そういえば、私たちが普段つかっている道具でも、どこかに壊れやすい部分が必ずあるものだ。たとえば、ドアは戸板よりもちょうつがいなど動く部分の方が壊れやすい。開け閉めするたびに負荷がかかるので、壊れやすいのは仕方がない。壊れにくいようにと、ちょうつがいをふやすと費用がかかる。つまり、丈夫さと費用の間の「トレードオフ」の結果、今のドアがあるのだ。そこで、細胞でも脆弱な部分は、何らかの重要な機能を実現するためのトレードオフなのではないかと考えた。
それを調べるために、30個の遺伝子が細胞周期というシステムの中でどのような関係を持っているか見なおしたところ、上限の低い遺伝子が、ひと固まりのサブシステムとして取り出せることがわかった。このサブシステムは、CDK活性の周期変動のダイナミクスの根幹を担う部分である(図4下)。つまり、このサブシステムが脆弱なのは、そのダイナミクスのトレードオフであると考えられる。私は、この発見を一般化し、システムの中で上限の低い遺伝子を見つければ、そこには未知の重要な機能を実現するためのトレードオフが隠されているに違いないと考えている。
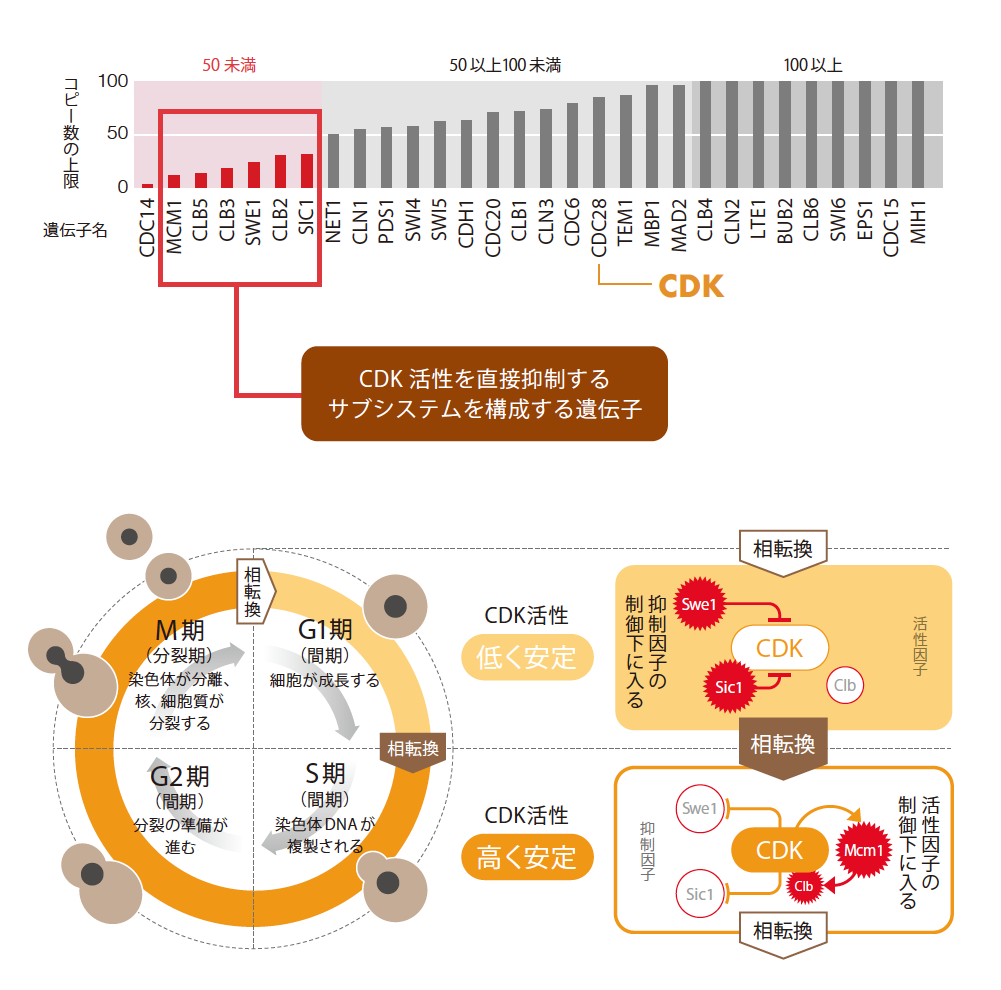
(図4) 細胞周期を動かす脆弱なサブシステム
(上)出芽酵母の細胞周期に関連する遺伝子30個のコピー数上限。gTOW実験で測定した(※コピー数100個以上の値は省略)。
(下)gTOW実験の結果、細胞周期を進める要となるCDKそのもの(CDC28 )は、発現量の変動に幅が許されるが、CDKの活性を安定して持続させ、相転換によって活性を切り替える制御システムは、コピー数上限の低い遺伝子のみで構成されていることがわかった。
もう1つの問いは、上限の高い遺伝子から生まれる。先に述べたコンピュータ酵母を使えば、「発現をどこまで上げても細胞が生きていられるか」というシミュレーションができる。その結果とgTOW実験のデータを比較してみると、コンピュータ酵母のロバストネスは実際の細胞よりもかなり低い(図5)。たとえばESP1という遺伝子のシミュレーションの結果は、実際の細胞での上限の数十分の一しかない。生きた細胞には、ESP1のロバストネスを高める「なぞ」が残されていることを示している。生きものは、これまでの研究の知識を合わせたモデルでは捉えられないしたたかさを備えているということである。こうして新たに見えてきた矛盾点を解明し、それをまたモデルに反映させていきたい。
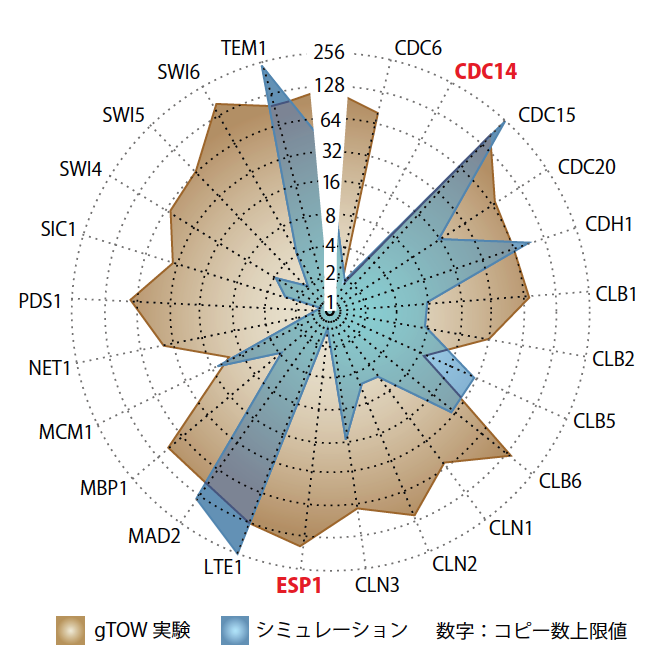
(図5) 生きた酵母とコンピュータ酵母のロバストネスの比較
gTOW実験で得られたコピー数上限値と、コンピュータ・シミュレーションによるコピー数上限値を重ねて表示した(円の外側に遺伝子名を表示)。
5.真核細胞に共通する避けられない脆弱性
真核細胞の細胞周期のダイナミクスを担う、CDKやその活性を制御する機構などは、酵母からヒトに至るまで非常に良く保存されている。それではgTOW実験でわかるような細胞周期のロバストネスも、同じように保存されているのだろうか。次はそれを考えた。
細胞周期のもう一つの有用なモデル生物に、分裂酵母(Schizosaccharomyces pombe )がある。分裂酵母はその名の通り増殖様式がシンプルな二分裂で、細胞周期のどこで異常がおきたのかを観察しやすい利点がある(図6)。
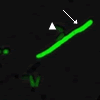
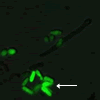
(図6) 分裂酵母で行ったgTOW 実験の顕微鏡写真
(左)mik1 が不均等に分配された細胞
(右)ほどよいコピー数をもつ細胞
遺伝子mik1 の過剰発現により分裂が阻害された細胞と、正常に分裂する細胞との違いがよく観察できる。緑色が濃く見える細胞ほど遺伝子のコピー数が多い。
出芽酵母と分裂酵母は同じ「酵母」に分類されているが、その分岐の起源は古く、進化的に両者はヒトと出芽酵母と同じくらい離れているとされる。
そこで私は分裂酵母でもgTOW法による実験系を作り、出芽酵母で調べた遺伝子と同じはたらきを分裂酵母で担うとされる30個の遺伝子(相同遺伝子)の上限コピー数を測り、両者を比べてみた(図7)。結果は、同じでもあり、違ってもいた。
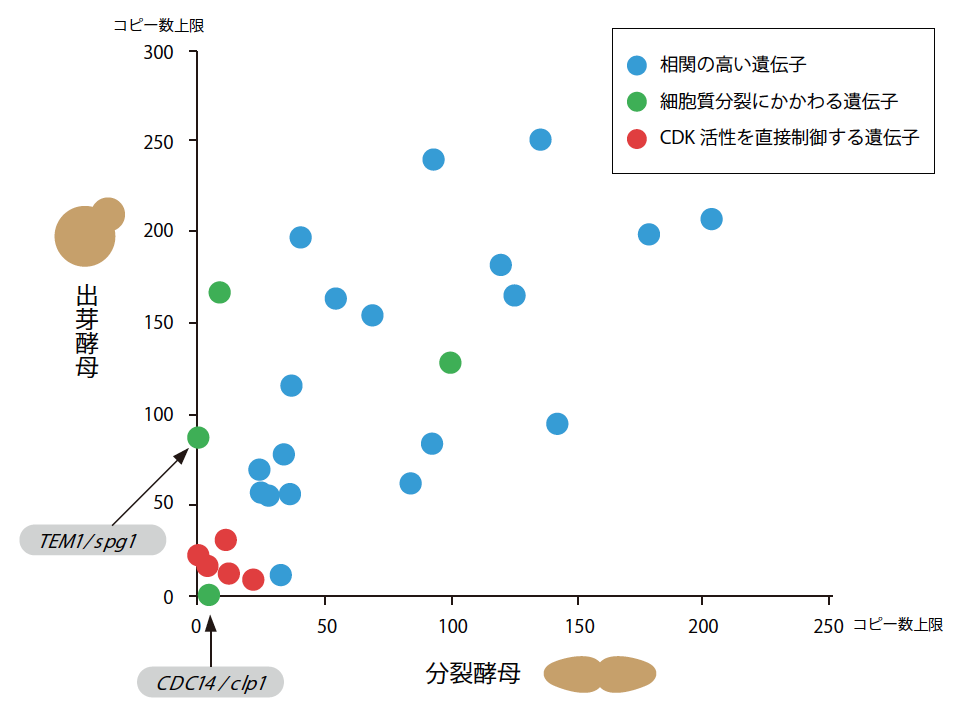
(図7) 出芽酵母と分裂酵母のロバストネスの比較
細胞周期に関連する遺伝子のコピー数上限値を2種の酵母で比べた。赤丸は、「脆弱なサブシステム」を構成する遺伝子。細胞質分裂に関連する2つの遺伝子をのぞけば、両酵母のロバストネスの分布は非常によく似ている。
出芽酵母で見たCDK活性の周期変動を担うサブシステムは、分裂酵母でも同じく脆弱だった。2種の酵母のロバストネスの比較により、真核細胞の細胞周期システムには、その根幹となるダイナミクスと引き換えに「避けられない脆弱性」が存在することが示されたと言ってよい。一方、細胞質分裂にかかわる遺伝子のうち2つは、出芽酵母ではロバストネスが高く、分裂酵母では低かった。出芽と分裂という分裂様式の違いは、ロバストネスの面でも多様性を見せていることもわかった。
ところで、両酵母の細胞周期で遺伝子発現の変動に対してもっとも脆弱な部分はどこかと見ていくと、どうやら「細胞質分裂」のようである。そこに関わるCDC14(出芽酵母)、spg1(分裂酵母)はともに上限が2コピー以下、つまり染色体にある本来の遺伝子に加えてたった1コピーふえただけで細胞が死んでしまう。細胞質分裂は、分裂期の最後、娘細胞に染色体が分配された直後の短い瞬間に、2つの細胞が切り離される過程である(写真)。この細胞周期の中で最もダイナミックな過程をうまく成し遂げるには、非常に微妙な遺伝子発現のバランスが必要であり、そのために細胞はロバストネスを犠牲にせざるを得なかったのだろう。
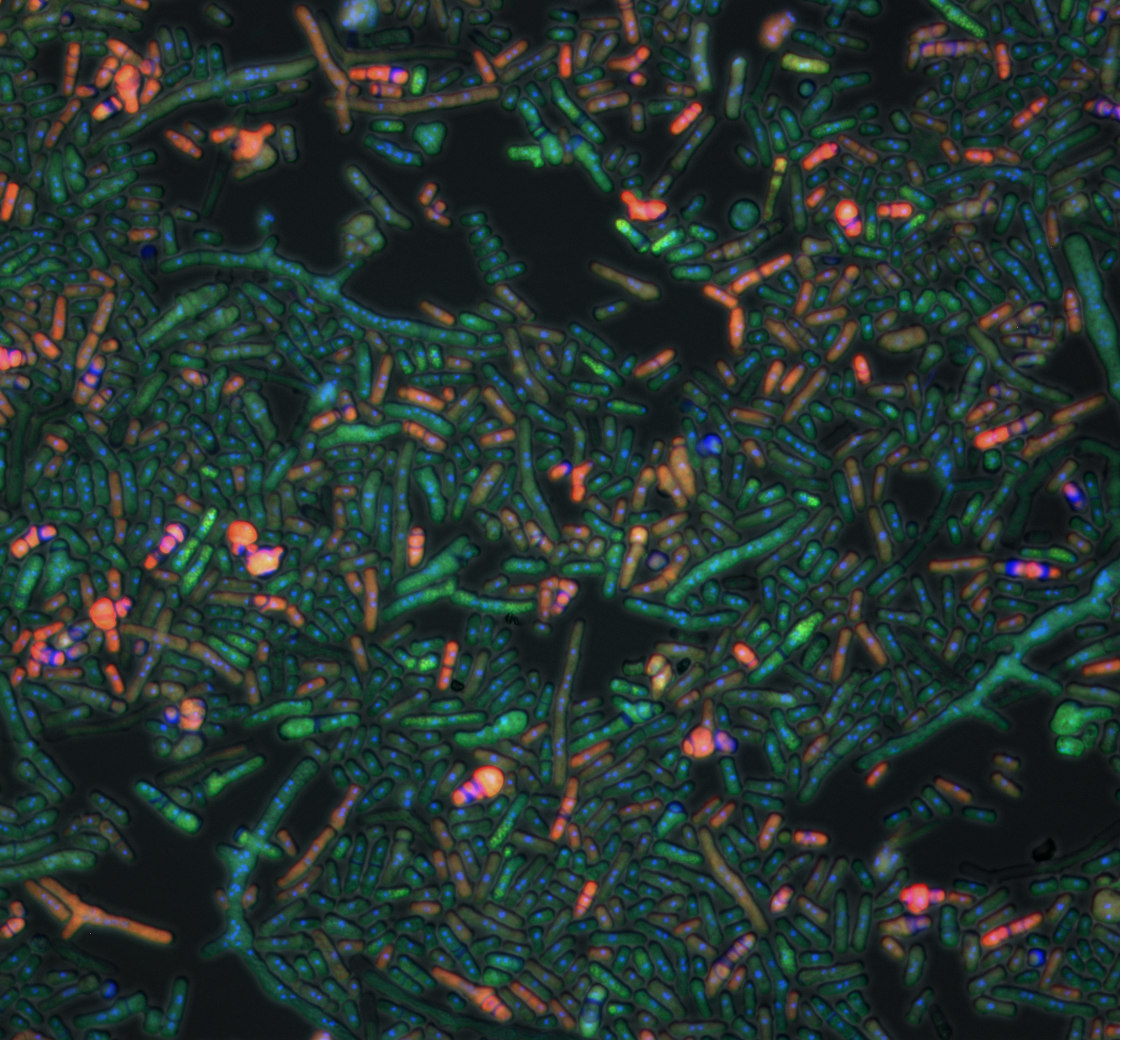
(写真)
遺伝子発現をうまく調節して細胞質分裂を進める分裂酵母。
6.生命がしたたかに続くしくみに学ぶ
ここまで話してきたのは、酵母という細胞が続いてきたしくみ、細胞周期というシステムのロバストネスについてであった。私はこのダイナミクスやロバストネス、そしてトレードオフという考え方は、人が作るシステムにも共通して適応できると思っている。人は、交通・機械・情報などの工学システムから、政治・経済・法律などの社会システムに至るまで、ありとあらゆるシステムを作る。そして、それぞれのシステムが続いていく過程で、弱点が発見され補われて、ロバストネスが高められていく。しかし、そのトレードオフとして、システムは膨大なリソースを要求するようになり、ダイナミクスを実現するための複雑さをどんどん増していく。
私は、生命が持つ最大の特徴は、限定された「リソースのしばり」の中でロバストネスを高めていった事による、洗練度の高さにあると思っている。人がシステムを作るときにも、有限のリソースからダイナミクスとロバストネスの最適のバランスを達成している生命から学ぶことは多いのではないだろうか。

守屋央朗(もりや ひさお)
岡山県生まれ。1998年神戸大学大学院自然科学研究科博士課程修了。ワシントン大学リサーチアソシエイト、科学技術振興機構ERATO研究員を経て、2006年よりさきがけ「生命システムの動作原理と基盤技術」領域研究者。癌研究所システムバイオロジー部のメンバーと研究中。
![[科学のコンサートホール]BRH JT生命誌研究館](/common/img/logo.svg)