RESEARCH
柔軟に変わる海馬の回路
記憶はちょっとしたきっかけで呼び起こされます。後ろ姿を見ただけで知り合いとわかるように、脳は記憶を頼りに一部の情報から欠けた情報を「復元」するのです。これを「パターン補完」と呼びます。さまざまな記憶が積み重なると、もう一つ「見分け」の能力が芽生えます。双子の兄弟が区別できるなど、小さな差異を見分けられるようになるのです。これを「パターン分離」と呼びます。一見、正反対にみえる補完と分離ですが、共に記憶に関わる海馬が関与していることがわかっています。
東京大学の池谷裕二さんは、神経細胞一つ一つの活動の個性に眼を向けるという新しい視点で海馬の神経回路を観察しました。そして、それがAND素子など電子回路に似た性質をもつことによって、補完と分離の能力が生まれていることを明らかにしました。そこには、神経細胞同士の結合の強さが変わる「シナプス可塑性」も関わっていました。
1.パターン補完とパターン分離
記憶を呼び起こすとき、たいていは何かがきっかけとなる。例えば、遠くから後ろ姿を見ただけで知り合いだとわかり、電話で声を聞いただけで「○○さんからだ」とわかる。下手な文字でも読めるし、手前の樹木で一部が隠れていても看板の字がわかる。脳は情報の断片から記憶全体を「復元」するのである。このプロセスはほぼ自動的に行われており、「パターン補完」と呼ばれている。過去の記憶が多ければ多いほど、また経験が豊かであればあるほど、うまくパターン補完ができるようになる。
記憶がさらに積み重なると、今までわからなかった微妙な違いに気づくようになり、「見分け」の能力が芽生えてくる。例えば、双子の兄弟が区別でるようになり、違いがわからなかったアイドルグループのメンバーがわかるようになる。マネとモネの絵やショパンとシューマンの曲も区別できるようになる。このように小さな差異を区別する能力を「パターン分離」と呼ぶ。
2.海馬の回路と電子の回路
「パターン補完」と「パターン分離」は、それぞれ情報の「統合」と「分解」に相当し、正反対の能力といってよい。しかし意外なことに、どちらの情報処理にも大脳辺縁系(註1)の一部である「海馬」が関与しているのである。海馬が傷害されるとパターン補完やパターン分離の能力が失われることからそれがわかる。ただし、海馬がどのようにして情報の統合と分解を行なっているかは、これまでのところ不明である。
電子回路では、情報の統合と分解はAND、OR、XOR素子のような論理演算子によって行われている。海馬も入力された情報を処理して出力する演算装置と見なすことができるので、論理演算子に基づいた回路が海馬にも存在するという仮説を立てて実験を進めた(図1)。

(図1) 海馬と電子回路
海馬は記憶と学習に深く関与する脳部位である。電子回路では、例えば図に示したような論理演算子が使われている。海馬にも電子回路の演算子のような性質がそなわっていることが予想される。
(註1) 大脳辺縁系
解剖学的には、大脳皮質の内側にあり、脳幹の上部に位置する。海馬を含めた、扁桃体や帯状回などがこれにあたる。
3.機能的多ニューロンカルシウム画像法で観る海馬の回路
海馬回路を一つの巨大な演算子と考えて、ラットの海馬切片の歯状回に切り込みを入れ、AとB2ヶ所の刺激部位を設けた(図2a)。2カ所からの入力刺激がどのように統合あるいは分解されるかを、出力部位となるCA1野において、錐体細胞(註2)の活動(発火)パターンとして観察した(図2a)。
多数の細胞の発火を一斉に記録するために、機能的多ニューロンカルシウム画像法(functional Multineuron Calcium Imaging, fMCI)という新しい方法を用いた。fMCIは、カルシウム蛍光指示薬を用いて、発火による細胞内カルシウム上昇を捉える可視化法である。私たちは、図2bで示した装置を用いることによって、毎秒2000 画像の高速で、数百の神経細胞の発火を一斉に撮影することを可能にした。

(図2) fMCI法を用いたラットの海馬の観察
(a) 歯状回のAとB2カ所から刺激を与え、CA1野の錐体細胞の活動を観察した。動画は、機能的多ニューロンカルシウム画像法を用いて、多数の細胞の発火パターンを高速撮影したもの。
Kimura, R. et al., J Neurosci, 31(37), 13168-13179 (2011) より改変
(b) 背面照射型の電子増倍冷却CCDカメラ、高開口数の対物レンズ、ニポウディスクを用いることによって、数百の神経細胞の発火を一斉に高速撮影することが可能となった。加えて、細胞に対する光毒性とカルシウム蛍光指示薬の光退色を軽減できた。
(註2) 錐体細胞
大脳皮質と海馬にある興奮性の神経細胞(ニューロン)のこと。海馬のCA1およびCA3領域の主要な神経細胞である。
4.見いだされた多様な演算子
単独刺激AとB、同時刺激A&Bという3種類の刺激を与えると、図3に見られるような発火パターンを示した。これをもとに、歯状回からCA1野につながる回路演算子が、AとBの入力情報をどのように統合、あるいは分解しているのかを解析するのである。

(図3) 神経細胞の発火応答とその空間分布
左には、特定の刺激(単独刺激A、単独刺激B、同時刺激A&B)を与えた場合の、183個の神経細胞の発火応答を示した。実験では同じ刺激を10回ずつ与え、細胞ごとの平均発火確率を求めた。
右には、細胞ごとの平均発火確率を、CA1野の神経細胞の空間分布に重ねて示した。
Kimura, R. et al., J Neurosci, 31(37), 13168-13179 (2011) より改変
細胞ごとに観察される発火確率の組み合わせは多様であり、結果として多彩な演算子が観察された。発火確率を統計学的に評価することで、以下のような5種類の演算子に対応する神経細胞が、特定の割合で存在することが明らかになった(図4)。つまり、単独刺激Aに選択的に反応する演算子(A)、単独刺激Bに選択的に反応する演算子(B)、単独刺激AにもBにも反応する演算子(OR)、同時刺激A&Bで、単独刺激AおよびBによる発火確率から期待される発火確率よりも高い確率で発火する演算子(AND)、そして同時刺激A&Bで、期待発火確率よりも低い確率で発火する演算子(XOR)である。以上の結果は、海馬の神経回路がAND、OR、XOR素子などの論理演算子にもとづいた情報演算を行うことを示している。このような解析は初めてである。
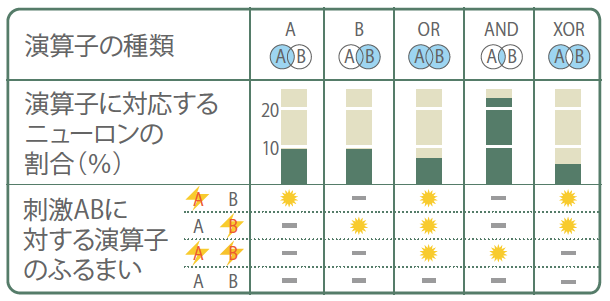
(図4) 見いだされた論理演算子とそれに対応する神経細胞の割合
神経細胞の発火応答を演算子の種類にしたがって分類した。それに対応する神経細胞の割合を示し、下段には演算子のふるまいを示した。
Kimura, R. et al., J Neurosci, 31(37), 13168-13179 (2011) より改変
5.シナプス可塑性によって変わる演算子
次に、シナプス可塑性を誘導することによる演算子の変化を検討した。シナプス可塑性は、特定の刺激によってシナプス結合の強さが強まったり弱まったりする現象であり、記憶と学習の基礎過程とされている。AとBの刺激を同時に、あるいは10msの時間差で連続(1Hz、20回)して与えることによってシナプス可塑性を誘導したところ、これらの連続刺激によって演算子が空間的に再編成されることがわかった。発火パターンを細胞ごとに見ると劇的ともいえる多様な変化を示したが、それはランダムな変化ではなく、集団として特定の傾向をもっているのである。
図5aを見てほしい。全体的な傾向としては、同時刺激A&Bにしか反応しなかった神経細胞が、同時刺激によるシナプス可塑性の誘導によって、単独刺激AとBのいずれにも反応するようになった(赤点線の囲み)。これは、入力差分よりも小さな差分として出力する演算ユニットが出現し、情報の統合が行われるようになったことを示す。一方、10msの時間差刺激においては(図5b)、単独刺激AにもBにも反応するようになる場合と(赤点線の囲み)、単独刺激AかBのどちらかのみに反応する場合があった(青点線の囲み)。これは、入力差分よりも小さな差分として、また大きな差分として出力する演算ユニットが出現し、情報の統合と分解が同時になされるようになったことを示す。

(図5) シナプス可塑性による論理演算子の変化
2種類(同時と時間差)の刺激後における、単独刺激AとBに対する発火確率の変化を示した。矢印の向きと長さは、2種類の刺激後における発火確率の変化の方向と度合いを示している。図中の疑似色は変化した神経細胞の相対的な個数を表し、暖色系の領域では応答する神経細胞が増えたことを示している。
Kimura, R. et al., J Neurosci, 31(37), 13168-13179 (2011) より改変
以上の結果から、同時入力が繰り返されると、情報を統合する方向に演算子が変更され、時間差のある入力が繰り返されると、情報をより分解する方向に演算子が変化することがわかった。日常に引きつけると、例えば姿と声を同時に体験することが繰り返されると(同時入力)、声だけでその人を思い出すことができ、互いを交互に見比べることを繰り返すと(時間差入力)、双子の差がわかるようになるということになる。
6.メゾスコピックな視点から観る海馬
以上の私たちの研究により、海馬回路には多様な論理演算子が存在していることが明らかになり、AND素子などを用いた並行分散型の情報処理を行っていることが示唆された。また、シナプス可塑性によって発火パターンと論理演算子が入力刺激依存的に変化したことから、情報演算のスタイルは柔軟に変化することも示唆された。
本研究は、個性ある要素と複雑集合体であるシステムという、異なる次元の実験データを系統立てて扱うための第一歩であると考えている。ミクロの個々の細胞とマクロのシステムをつなぐメゾスコピックな視点から、記憶と学習の素過程であるシナプス可塑性を捉え直すことが可能になったからである。これを、情報演算に基づいた中枢神経疾患の病因解明や治療方法の確立につなげたいと考えている。

池谷裕二(いけがや ゆうじ)
1998 年東京大学大学院薬学系研究科にて博士号を取得。コロンビア大学客員研究員、JSTさきがけ研究員などを経て、東京大学大学院薬学系研究科准教授。同大学総合文化研究科連携准教授。
![[科学のコンサートホール]BRH JT生命誌研究館](/common/img/logo.svg)