細胞・発生・進化研究室

生命現象を再現する数理モデル

生命現象の解明に使われる数理モデルを紹介し、それら数理モデルのコンセプトや構造や数式も含めて説明します。
 

下で紹介しているCell vertex modelの単純なバージョンを実際に動かせるページをGoogle Colabを使って公開しています。

外部ページ(Google Colab)へのリンク
 

1. クモ胚の形態変化を再現した仮想多細胞体モデル

・胚の形態形成を表現するCell vertex model

図１の数理モデルは、クモの初期胚発生を再現するためにコンピュータ上で球面上に細胞を並べて構築されたものです。このモデルの基本となる数理モデルは、 Cell vertex modelと呼ばれるものを使っています。 Cell vertex modelは、多細胞組織の変形を細胞に基づいた動きから再現することをコンセプトに、上皮細胞を始め生物の組織-器官-個体の形態形成の多くの数理研究に用いられています。Cell vertex modelの基本構造は、細胞を多角形で表現し、その細胞が多数敷き詰められることで多細胞組織を表現します(図２)。

図１ 実際のクモ胚の形態形成と数理モデルでのクモ胚の形態形成　

動画の左:実際のクモ胚、動画の右：数理モデルのクモ胚　
 

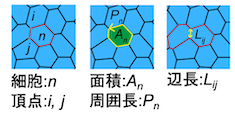
図２ 数理モデルでの細胞の表現

細胞と各頂点ごとに番号が振られ、細胞は面積や辺の長さや周囲の長さの情報を持っています。

 

各多角形の各頂点が、細胞の力学的な特徴を反映した以下の式(1)を基に、運動方程式(2)に従って位置を時間変化させることで、細胞の変形が起こり、それに従い生物組織の形態形成を再現することができます。細胞が持つ力学的な性質として、細胞成長、細胞収縮、細胞接着を導入し(図３)、細胞が持つエネルギー式(1)は次の式で表されます。

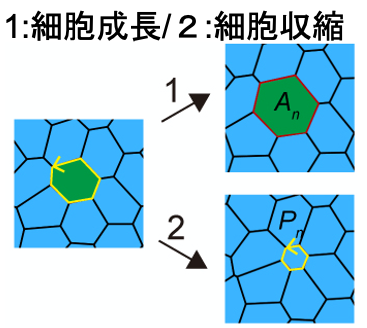
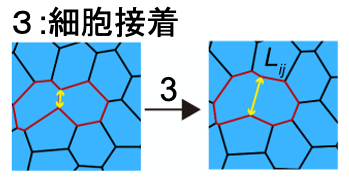
図３　細胞が持つ力学的な性質

細胞の力学的な性質の分子背景として、細胞成長は細胞内のフィラメントによる細胞骨格に、細胞収縮はアクチンリングに、細胞接着はカドヘリンなどの接着分子に由来します。

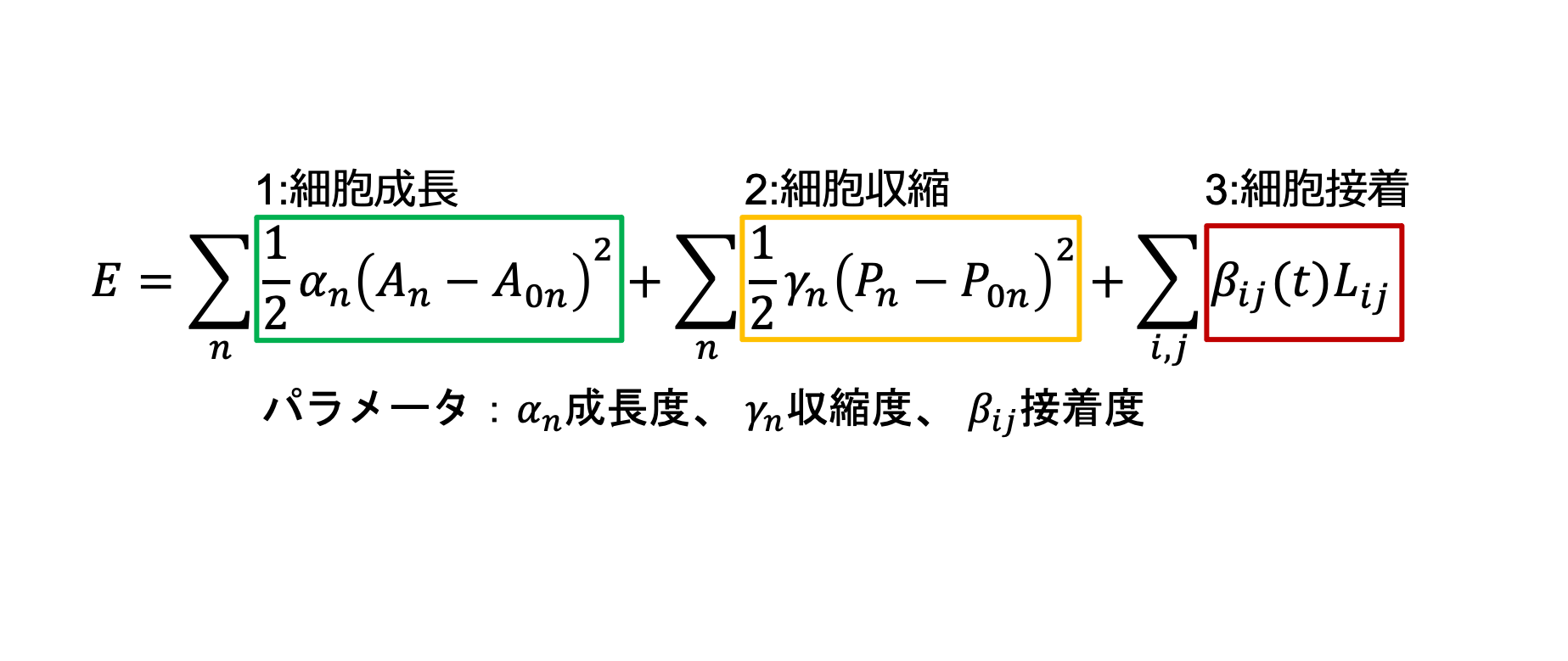
式１ 細胞が持つエネルギー

細胞が持つエネルギー式は、第１項の細胞の面積の弾性力、第２項の細胞の周囲長の張力、第３項の細胞の辺の接着力で表現されます。

細胞の時間経過による変形を計算する運動方程式(2)は次の式で表されます。

式2 細胞の各頂点が従う運動方程式

一般的な運動方程式では、慣性項がありますが、細胞の変形はそこまで速い変形ではないと仮定して、慣性項を無視しています。